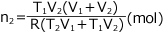理論化学
化学講座 第37回:分圧の法則と2気体の混合
理想気体は相互作用を及ぼさないのでした。ということは、二種類の気体が混合されている気体を考えるとき、一種類ずつ別々に気体の圧力を求める事ができるのです。お互い干渉しないのだから、別々に求めてもいいのです。
そして、その圧力の和を取れば気体全体の圧力を求めることができます。
例として、下図のように nA (mol) の気体 A と Bn (mol) の気体 B が混合された混合気体を考えます。
この混合気体が体積 V (L) の容器に封入されて温度 T (K) に保たれているとして、この混合気体の作る圧力を考えてみましょう。
理想気体の状態方程式より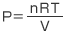 です。
です。
よってAのつくる圧力は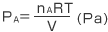
Bのつくる圧力は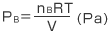 となります。
となります。
従って、この気体のつくる圧力は となります。
となります。
ここでPAをAの分圧、PBをBの分圧Pを混合気体の全圧といいます。
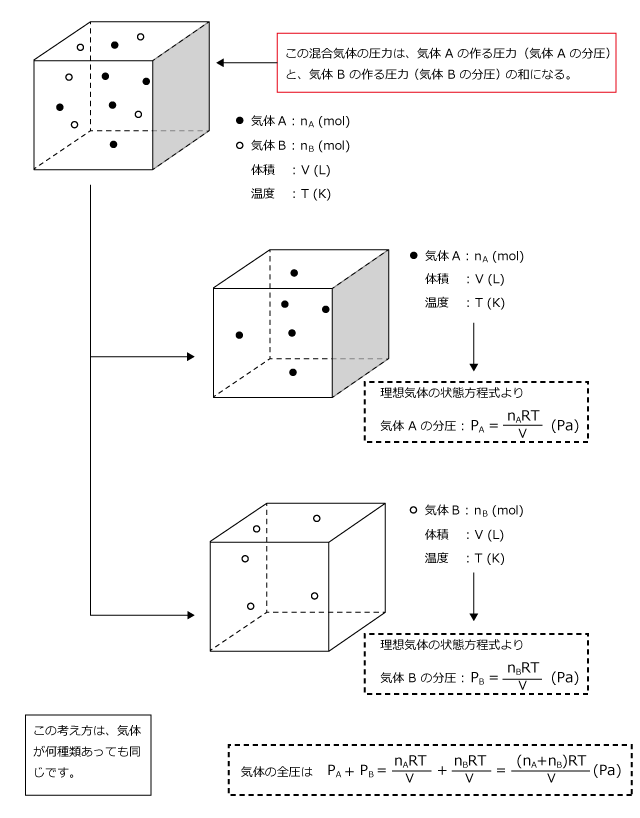
この式から、気体の圧力は体積や温度が同じであれば、気体の種類によらず物質量によってのみ決まる。ということが再確認できますね。
ですから、この問題であれば、混合気体の物質量の総和が 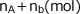 であることから直接、
であることから直接、
(混合気体の圧力) = 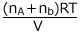 と求めても問題はありません。ただ、理想気体では構成する気体の分圧の総和が全圧になるという考え方で理解しておくことが大切です。
と求めても問題はありません。ただ、理想気体では構成する気体の分圧の総和が全圧になるという考え方で理解しておくことが大切です。
化学反応の量的関係で物質量のかわりに分圧を用いる
反応前後の温度と体積が同じであれば、分圧は物質量に比例するので、気体反応の量的関係の計算(反応物の消費量、生成物の生成量などの計算)をするとき、物質量に直さずに分圧で計算をすることができます。
例えば、A + B → C という反応を考えてみましょう。V (L)、T (K) に保たれた容器に、![]() の気体 A と、
の気体 A と、 ![]() の 気体 B を入れて反応させたとします。A が完全に反応した後の容器内の全圧を求めてみましょう。ただし
の 気体 B を入れて反応させたとします。A が完全に反応した後の容器内の全圧を求めてみましょう。ただし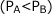 とします。
とします。
まず、物質量を求めてから考える方法でやってみます。
気体の状態方程式より、A の物質量は、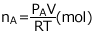 、B の物質量は
、B の物質量は 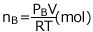 です。
です。
( ここで、![]() なので、
なので、![]() ですね。反応後は A が全部なくなって、B が一部残ります。 )
ですね。反応後は A が全部なくなって、B が一部残ります。 )
化学反応式より、反応前後の物質量は以下のように求めることができます。
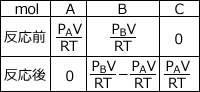
反応後の物質量は、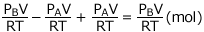 ですね。
ですね。
ここから、反応後の全圧は、![]() と求まります。
と求まります。
この解き方、どう思いますか? 表の値は全部![]() がついていますが、これは最初に圧力から物質量を出すときにくっついた値です。そして、最後にこれを外して圧力を求めているのですから、二度手間ですよね。
がついていますが、これは最初に圧力から物質量を出すときにくっついた値です。そして、最後にこれを外して圧力を求めているのですから、二度手間ですよね。
これを省略したって問題はないはずです。
そこで、分圧を物質量の代わりに用いて考えてみます。

よって、反応後の全圧は 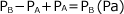
では、問題をやってみましょう。
問題
容積 1.0 L、温度 27 ℃ の容器に 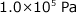 の CO と
の CO と 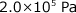 の
の ![]() を封入して完全に反応させた。
を封入して完全に反応させた。
反応した後の温度は 27 ℃、容積は 1.0 L だった。反応後の気体の全圧はいくらか。
解説
この問題を解くにあたって、理想気体の状態方程式を用いて CO と ![]() の物質量を求め、
反応後の
の物質量を求め、
反応後の ![]() と
と ![]() の物質量を出して、それから理想気体の状態方程式を再度用いて・・・ 。
というプロセスで解くと、2 回も理想気体の状態方程式を解くことになって大変です。そこで、さっき説明したように、分圧を使って反応後の圧力を求めましょう。
の物質量を出して、それから理想気体の状態方程式を再度用いて・・・ 。
というプロセスで解くと、2 回も理想気体の状態方程式を解くことになって大変です。そこで、さっき説明したように、分圧を使って反応後の圧力を求めましょう。
反応式は 2CO + ![]() → 2
→ 2![]()
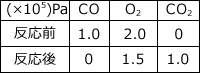
よって、反応後の全圧は、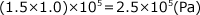
すごく楽に解けましたね。実は、このやり方は、反応後に温度や体積が変わっても使うことができるのです。
問題を解きながら、やり方を説明します。
問題
容積 1.0 L、温度 27 ℃ の容器に 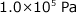 の CO と
の CO と 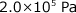 の
の ![]() を封入して完全に反応させた。
を封入して完全に反応させた。
反応した後の温度は 227 ℃、容積は 1.0 L だった。反応後の気体の全圧はいくらか。
解説
一度に反応後の圧力を求めず、いったん27℃のまま反応が終わって、それから227 ℃に温度が上がったと考えればいいのです。
下のように表を一段増やします。ここで、27 ℃ (300 K) で反応が終わってから温度を上昇させて227 ℃ (500 K)にすると、シャルルの法則から、圧力は ![]() 倍になります。
倍になります。

上表より、反応後の全圧は、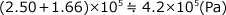
反応後の容積が異なる場合も同様にして考えることができます。同温、同体積で反応が起こると仮定して反応後の圧力を求め、そのあとボイルの法則やシャルルの法則を使って温度や体積を変えればよいのです。
コックでつながれた容器に入った2気体の混合
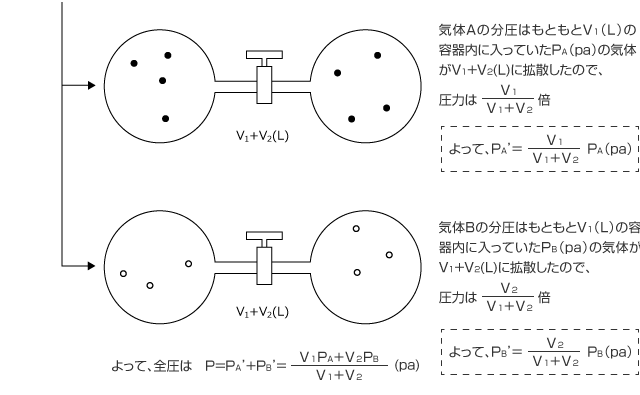
下図のように体積の無視できる細い管でつながれた二つの容器の中に封入された気体の混合後の圧力について考えてみましょう。よくある問題ですよね。この問題は、コックを開けた後の気体を 1 つのまとまったものと考えずに、左側に入っていた気体と右側に入っていた気体を別々のものとして扱うとうまく行きます。
複雑な事象の場合、独立したいくつかの事象に分解することによってとらえやすくすることができますが、これはそういう考え方の 1 つですね。気体A、気体Bを別々に考えましょう。
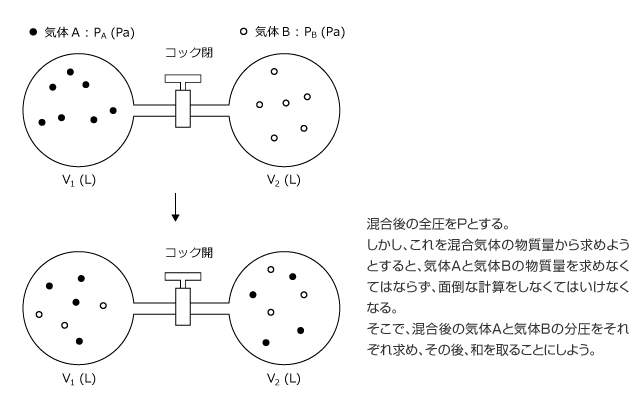
最後に、先ほどの容器のコックを開けて全圧がP (Pa) になるまで気体を入れ、左右を違う温度にしたら各容器はどのような圧力になるか。また、各容器に入っている気体の物質量は何 (mol) かを考えてみよう。
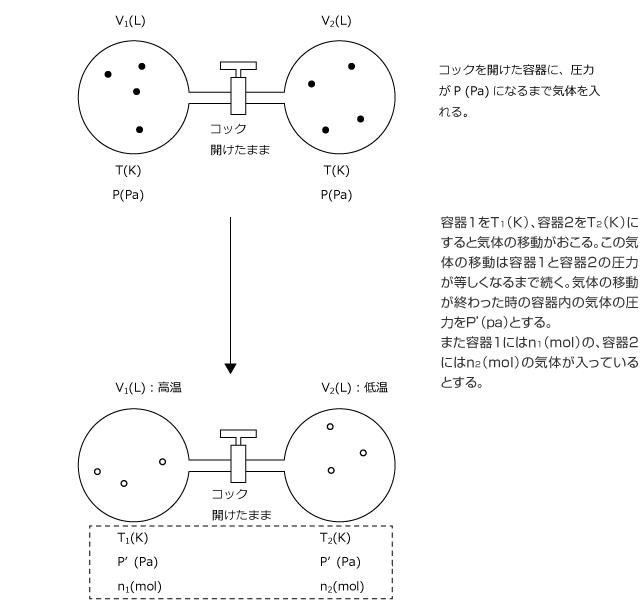
未知の値を求めるためには、その値に関する連立方程式を作って解けば良いのですが、この条件でどういう式が成立しているか、考えてみましょう。
①容器1と容器2に入っている気体の圧力は同じ
圧力に差があれば気体の移動がおこりますから、コックがあいていれば2気体の圧力は等しくなります。
②容器1と容器2に入っている気体の物質量は不変
状態変化や容器から容器への移動をしても前後で物質量や質量の総和は変化しない。
これを物質量保存則、質量保存則という。
- 容器1と容器2の圧力について
それぞれの容器について気体の状態方程式を立てると、圧力をP'(Pa)
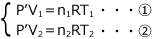
- 物質量保存則について
もともと
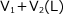 の容器に、T (K)、P (Pa) の気体が入っていたので、気体の総物質量は気体の状態方程式より気体の物質量は
の容器に、T (K)、P (Pa) の気体が入っていたので、気体の総物質量は気体の状態方程式より気体の物質量は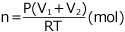
よって
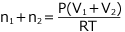 ・・・ ③ が成立する。
・・・ ③ が成立する。
①、②、③を連立方程式をして解けばよい
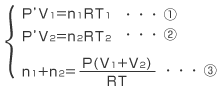
①より 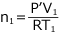 ・・・①' ②より
・・・①' ②より 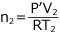 ・・・②' これらを ③ へ代入して
・・・②' これらを ③ へ代入して
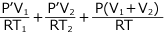
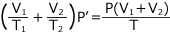
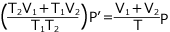 よって、
よって、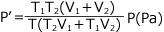
①'より 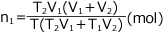 ②'より
②'より