理論化学
化学講座 第33回:熱化学方程式③【熱化学方程式の解き方】
今回は、いくつかの熱化学方程式を組み合わせて、ある反応で生じる反応熱を求める方法について説明します。これには、前回説明したエネルギー図を用いる方法と、代数的に処理する方法があります。まずは、前回の最後に説明したエネルギー図を復習しておきましょう。
物質の持っているエネルギーを図で表したものがエネルギー図でした。前回は以下の①~③の熱化学方程式についてエネルギー図を作ってみましたね。
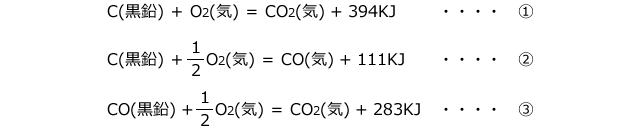
この3つの熱化学方程式をエネルギー図に表してみると、C(黒鉛)が直接CO2(気)になる経路①も、一旦CO(気)になってからCO2(気)になる経路②も熱量の総和は一定である事が分かります。このように、反応熱の総和は経路によらず、最初と最後の状態のみで決定されますが、この法則をヘスの法則といいました。
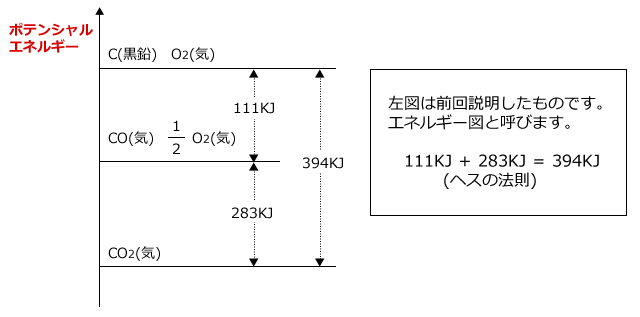
この図を見てみると、① ~ ③のいずれか1つの反応熱が分かっていなかったとしても、他の2つの反応熱からそれを求める事ができるのがわかりますね。
たとえば、②の熱量が分からないとします。
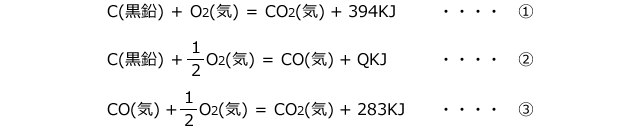
分からないので、仮に②の反応熱をQKJとしておきます。そして、エネルギー図にそれを入れてみると、下図のようになります。

ヘスの法則より、①の経路も②、③の経路も熱量の総和は同じになりますから、394 = Q + 283 となります。これを解けば、Q = 111KJ となり、CO(気)の生成熱が111KJ/molである事が分かります。これが、エネルギー図を用いた熱化学方程式の解き方です。